algo2

Sessió en línia del dia 7/12/2020: Enumeratius / Backtracking

Un algoritme enumeratiu és aquell que garanteix l’obtenció de la millor solució, l’òptim, per la via d’explorar tot l’espai de les solucions possibles. La sortida del mètode consisteix en enumerar totes les solucions òptimes.

Tenim diverses tècniques per tal de trobar aquestes solucions:

El backtraking: El backtracking és una tècnica algorítmica que ens permet resoldre problemes de forma recursiva, intentant construir una solució de manera incremental, eliminant totes aquelles solucions parcial, (retrocedint/backtrack) que no compleixen les limitacions del problema, tan aviat com es determina que la solució no es pot completar com a solució vàlida/òptima. Malauradament, un algorisme de backtracking pot passar molt de temps explorant parts de l’espai de possibles solucions que no donen lloc a una solució vàlida i/o òptima.
Ramificació i poda (Branch and Bound): Un procediment enumeratiu basant en ramificació i poda requereix definir una funció d’avaluació per a cada node, per així seleccionar en cada pas quin és el millor node a explorar, i per altra banda eliminar certs nodes a ser explorats (aquells que no arribaran a la solució òptima). L’eficiència del mètode anirà fortament lligat a la funció que avalua cada node.

Backtracking

Pensem amb el problema de la motxilla mitjançant la tècnica del backtracking.

Fins ara hem resolt aquest problema amb diverses solucions:

Força bruta
Greedy
Programació dinàmica

Si tinguéssim els següents 5 objectes:

	Weight	Weight
Object 1	2	40€
Object 2	3.14	50€
Object 3	1.98	100€
Object 4	5	95€
Object 5	3	30€

Amb la força bruta hauríem d’explorar totes les possibles solucions i avaluar-les així com és mostra a la següent imatge.

Brute force

Podem optimitzar la solució aconseguida mitjançant el Backtracking. Com hem dit abans, el backtracking és una estratègia recursiva que crearà la solució de forma incremental explorant totes les possibles solucions del problema, però descartant aquelles que no puguin arribar a una solució òptima donat unes restriccions i objectiu definit. En el cas del problema de la motxilla, podem utilitzar el DFS per tal d’explorar l’arbre de solucions. Si arribem a una solució parcial on la solució ja no és factible, no caldrà continuar explorant. En aquest problema, com més gran és el nombre d’articles o menor la capacitat de la motxilla, més gran és la millora experimentada per l’algoritme basat en backtracking. Pensem dons una solució amb backtracking.

Amb backtracking tenim tres punts importants:

Les eleccions.
Les restriccions.
L’objectiu.

En el cas del problema de la motxilla. Ens queda d’aquesta manera:

Les eleccions: Incloure o no incloure l’objecte.
Les restriccions: No pot superar un cert pes.
L’objectiu: Els objectes seleccionats han de tenir el màxim valor.

A la següent imatge podem veure l’arbre de solucions que exploraríem, aquells nodes marcats de color vermell indiquen nodes on la solució no és factible i per tant es para d’explorar. backtracking

A continuació podem veure el codi python pel problema de la motxilla mitjançant backtracking:

# max amount of weight allowed
max_weight = 23

# actual items
item_values = [16, 15, 4, 3, 2]
item_weights =[14, 13, 7, 2, 1]

# max no.of items available
num_items = len(item_weights)


def knapsack(current_weight=0, current_value = 0, index=0, items = []):
    
    # exit conditions
    if current_weight >= max_weight:
        return (current_value, current_weight,items)
    if index >= num_items:
        return (current_value, current_weight,items)
    
    # We have 2 cases (take/don't take)
    case1_value, case1_weight,case1_items = knapsack(current_weight + item_weights[index],
                                                     current_value + item_values[index], 
                                                     index + 1,items +[index])
    case2_value, case2_weight,case2_items = knapsack(current_weight, 
                                                     current_value, 
                                                     index + 1,items)
    return max([(v,w,items) for v,w,items in [(case1_value,case1_weight,case1_items),
                                              (case2_value,case2_weight,case2_items)] if w <= max_weight])
                                              
print(knapsack())                                           

Vídeo Sudoku via Backtracking

Esquema general d’un algoritme de backtracking

A continuació podem veure l’esquema general d’un algorítme de backtracking:

mapa

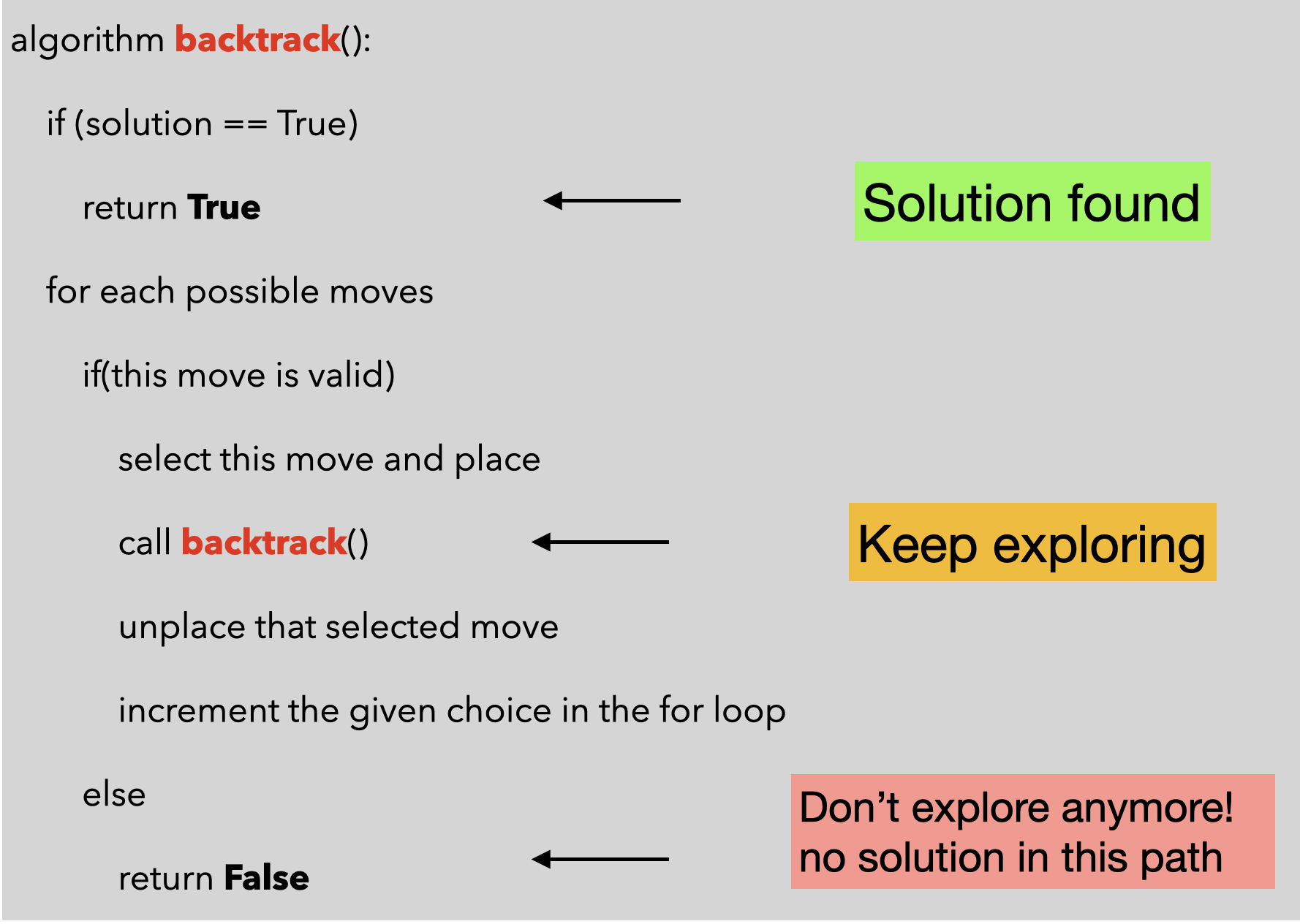
Així com ilustra l’imatge, els algorítmes de backtracking tenen 3 parts importants: 1) comprovar si hem arribart a una solució vàlida; 2) Si la solució és vàlida explorar; 3) si la solució no és vàlida parar l’exploració.

Exercici: Pinta el mapa

Donat el següent mapa:

mapa

Es demana trobar un algoritme que ens doni totes les possibles solucions existents si volem pintar el mapa utilitzant únicament 3 colors (blau, verd, vermell) amb la restricció que dues regions que comparteixen frontera no poden compartir el mateix color.

Exercici: Collecting Beepers

https://open.kattis.com/problems/beepers