algo2

Sessió en línia del dia 20/12/2020: Enumeratius / Ramificació i Poda

Els algoritmes de ramificació i poda (branch and bound en angles) implementen l’algoritme de backtracking, però no a la inversa. Els podem veure com una variant millorada del backtracking aplicada majoritariament a problemes optimització combinatoria o matemàtica.

L’objectiu de la ramificació i poda consisteix amb reduïr l’espai de cerca, explorant primer aquelles solucions més prometedores i descartant durant el procés totes aquelles solucions parcials que no puguin produir una millor solució de l’obtinguda fins aleshores. Per a realizar això, s’introdueixen unes cotes que ens ajudaran a escollir la solució a explorar i rebjutar-ne d’altres. A diferència del backtracking, aquí no limitem l’exploració del graf a cap algoritme en particular. L’exploració del graf anirà regida en funció de les cotes obtingudes.

Un dels punts principals dels algoritmes de ramificació i poda és trobar i definir una funció que determinarà la cota inferior i/o superior al problema optimització que volem resoldre. Un cop definida aquesta funció s’explora el node més prometedor en cada etapa i es rebutja (poda) l’exploració de tots aquells nodes quan la cota superior és menor (o bé la cota inferior és major en cas d’un problema de minimització) a una solució ja trobada.

Que ens dieuen les cotes:

• La cota superior ens indica la solució màxima que podriem (no assegura) arribar a trobar si seguim el node donat.

• La cota inferior ens indica la solució mínima que podriem (no assegura) arribar a trobar si seguim el node donat.

• En problemes de maximització, ens interessa explorar tots aquells nodes on la seva cota superior sigui més gran que la millor solució trobada fins el moment
• En problemes de minimització, ens interessa explorar tots aquells nodes on la seva cota inferior sigui més petita que la millor solució trobada fins el moment

El pseudocodi d’un algoritme de ramficació i poda pot seguir el següent esquema:

function branch_and_Bound():
    activeset = {}
    bestsolution = Null
    while( activeset not empty):
        choose the most promising branching node k, node k  \in activeset
        remove the node k from activeset
        generate the children of node k and estimate the bounds
        for each child i of node k
            if(upper bound of child i is worse than bestval):
                  kill child i
            elif(child i is a complete solution):
                  bestval = solution from child i
            else:
                  add child i to activeset
              

---

Exercici: Problema de la motxilla

La setmana passada vam veure com podíem resoldre el problema de la motxilla mitjançant un algoritme de backtracking. Aquesta setmana veiem com encara podem millorar la solució d’aquest problema mitjançant un algoritme de ramificació i poda.

La idea principal recau en el fet que ho podem fer millor (que amb el backtracking) si coneixem una cota que ens indica quina és la millor solució que podriem arribar a trobar si explorem el subarbre d’un node donat. Aquesta informació és ajudarà a decidir el següent node a explorar i parar-nos si ja no tenim cap possiblitat de trobar una solució millor. Si la cota d’un node en questió és menor que una solució ja trobada, podrem ignorar (podar) aquest node i tots els seus subarbres. Per tant, l’estratègia consisteix a calcular la cota superior (millor solució) per a cada node i comparem aquesta cota amb la millor solució trobada fins aleshores abans d’explorar el node.

Donat els següents objectes i una capacitat màxima de 15 Kg:

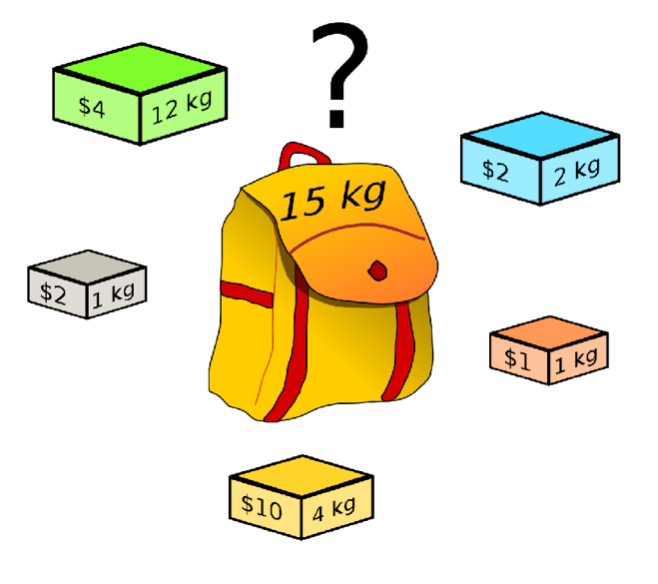
Els objectes estan ordenats amb el següent ordre: [verd, blau, vermell, groc, gris] Veiem pas a pas com podem fer-ho.

El primer que hem de fer és definir com calcularem la cota inferior i la cota superior. Les podem calcular de la següent manera:

• Cota superior: Agafem tots els objectes que individualment càpiguen dins la motxilla. En el nostre cas, donat que la motxilla té una capacitat màxima de 15kg, podrem considerar tots els objectes que individualment pesin menys de 15kg. Per tant, en el nostre exemple, la cota superior inicial equival a 4+2+1+10+2 = 19$.

• Cota inferior: Agafem els primers objectes de la llista fins a arribar a la capacitat màxima de la motxilla. En el nostre exemple, la cota inferior inicial equival a 4+2+1 = 7$.

A continuació podem començar:

• Primer pas: Trobem la cota inferior mitjançant una solució qualsevol. Com hem dit abans aquesta tindrà un valor de 7$.

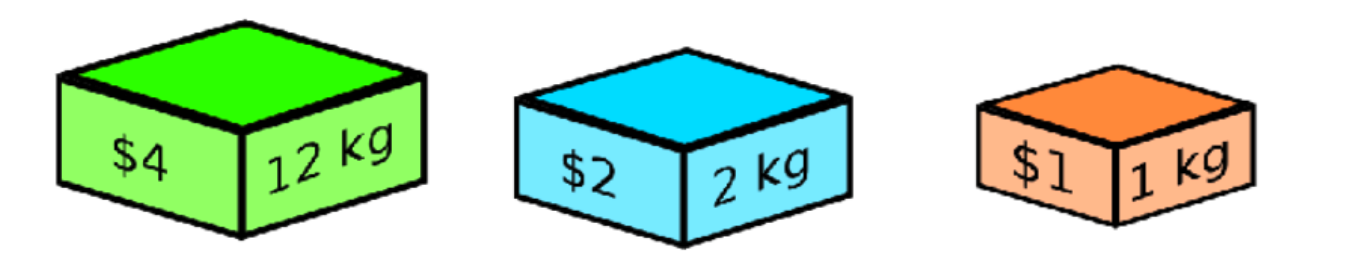
• Segon pas: Considerem un primer objecte, en aquest cas l’objecte de color verd amb un valor de $4 i pes de 12kg. Calculem la cota superior i inferior de les dues opcions (agafar i no agafar l’objecte) i en cas que la seva cota superior sigui millor que el millor resultat obtingut fins alehores afegim el fill a la llista de nodes a explorar.
  • Si agafem l’objecte verd:
    • Cota superior: 4$ + el valor de la resta d’objectes que individualment càpiguen dins la motxilla (4+2+2+1). Com podem veure, l’objecte groc no es considerat ja que la capacitat restant de la motxilla és 3kg i l’objecte groc pesa 4 kg. Cota Superior: 9$
    • Cota inferior: 4$ + el valor dels objectes següents fins arribar a la capacitat màxima. Cota Inferior: 4 + 2 + 1 = 7$
  • Si NO agafem l’objecte verd:
    • Cota superior: El valor de la resta d’objectes que individualment càpiguen dins la motxilla (2+10+2+1). Cota Superior: 15$
    • Cota inferior: El valor dels objectes següents fins arribar a la capacitat màxima. Cota Inferior: 2 + 10 +2 +1 = 15$

• Afegim les dues opcions dins la llista de nodes a explorar ja que la seva cota màxima és superior a la millor solució actual.

• Tercer pas: Decidim el següent node a explorar tenint en compte la cota inferior i/o la cota superior de tots els nodes actius. En el nostre cas tenim 2 nodes actius. Explorem el node corresponent a no agafar l’objecte verd, ja que aquest node té una cota superior més gran.

• Quart pas: Explorem el node seleccionat i avaluem la cota inferior i superior dels seus fills. Afegim a la llista de nodes actius els fills que tinguin una cota superior a la solució actual. En cas contrari, no afegim el node i per tant estem podant l’arbre de solucions.

• Quint pas: continuem iterant fins que tinguem nodes actius a explorar.

Podem utilizar la cota inferior per podar més l’arbre?

---

Exercici: Assignació de tasques:

Tenim 4 tasques i 4 empreses disponibles que poden realitzar-les. Cada empresa ens ha ofert una solució a cada una de les tasques amb un cost X. Volem assignar una única tasca diferent a cada empresa tal que el cost total sigui el mínim. El cost de les tasques per a cada una de les empreses està definit segons la següent taula:

	Tasca A	Tasca B	Tasca C	Tasca D
Empresa 1	11	12	18	40
Empresa 2	14	15	13	22
Empresa 3	11	17	19	23
Empresa 4	17	14	20	28

Trobeu la solució del problema mitjançant un algoritme de ramificació i poda.

Exemple:

• Empresa 1 - > tasca A
• Empresa 2 - > tasca B
• Empresa 3 - > tasca C
• Empresa 4 - > tasca D
• Cost total : 11+15+19+28 = 73

---

Exercici: Puzzle 8

Donat un taulell de 3x3 amb 8 números i un espai buit. L’objectiu és col·locar els números a les cel·les perquè coincideixin amb la configuració final. Podem lliscar les cel·les adjacents (dreta, esquerra, amunt i avall) a l’espai buit. Exemple:

Solució amb força bruta: Podem fer una cerca utilitzant el mètode DFS (Mirem de totes les configuracions d’un problema determinat, és a dir, tots els estats als quals es pot accedir des de l’estat inicial).

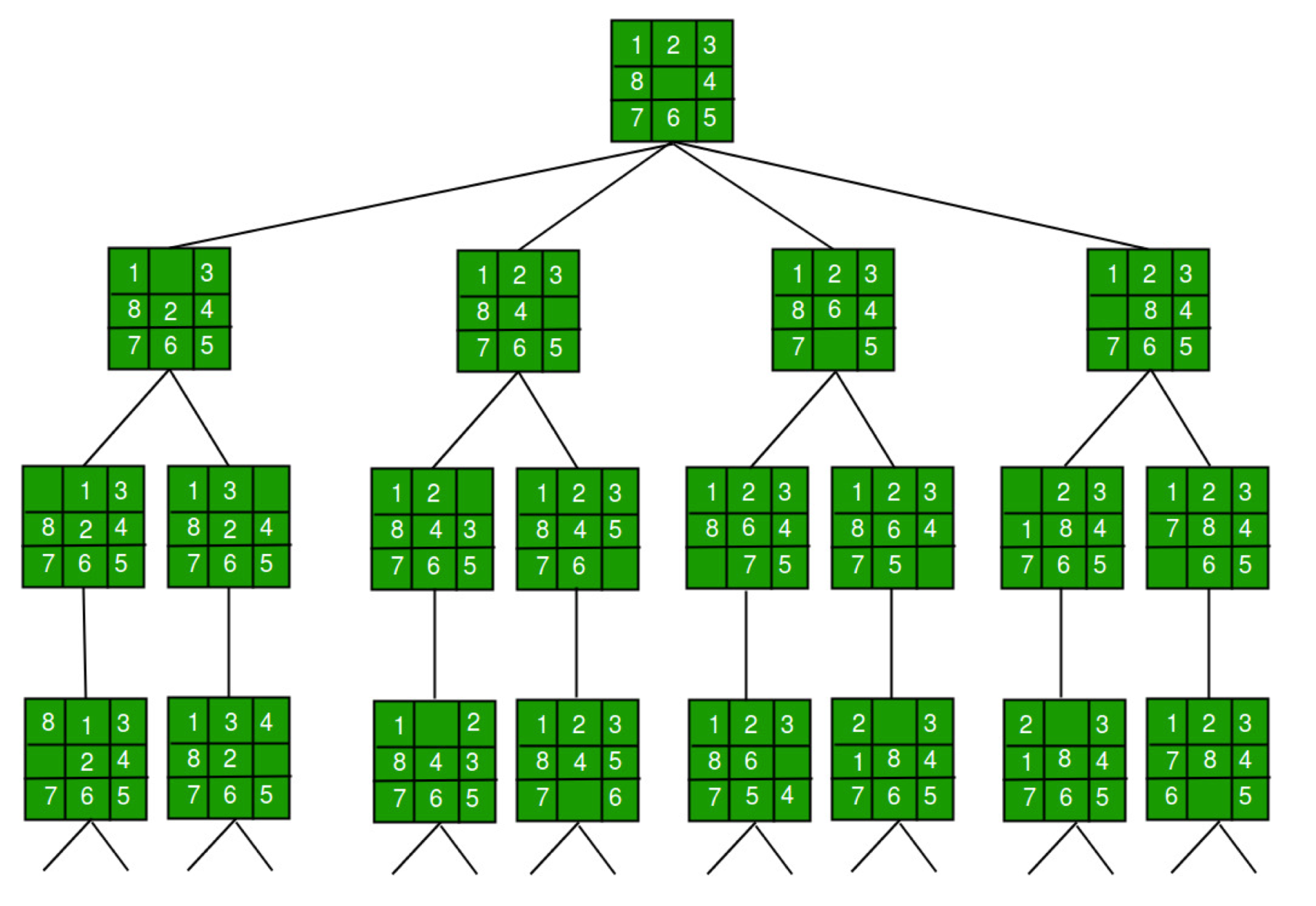Aquesta solució té un problema donat que els moviments successius ens poden allunyar de l’objectiu en lloc d’apropar-nos. Pot ser que no es trobi mai una solució amb aquest enfocament.

Solució amb ramificació i poda:

Penseu una solució mitjanaçant Ramificació i poda.

Estem en un problema de minimització, definirem una funció de cost que estimi la cota superior. La funció de cost la podem definir de la següent manera:

• C(X) = g(X) + h(X) on:
  • g(X) és el cost d’arribar al node X des de l’arrel. És a dir, el número de moviments realitzats fins aleshores.
  • h(X) és el cost d’arribar a una solució desde el Node X. Podem estimar el número de moviments mínims que s’han de realizar mirant el número de posicions on tinguem un número i aquest sigui diferent del número objectiu de la solució.

Exemple:

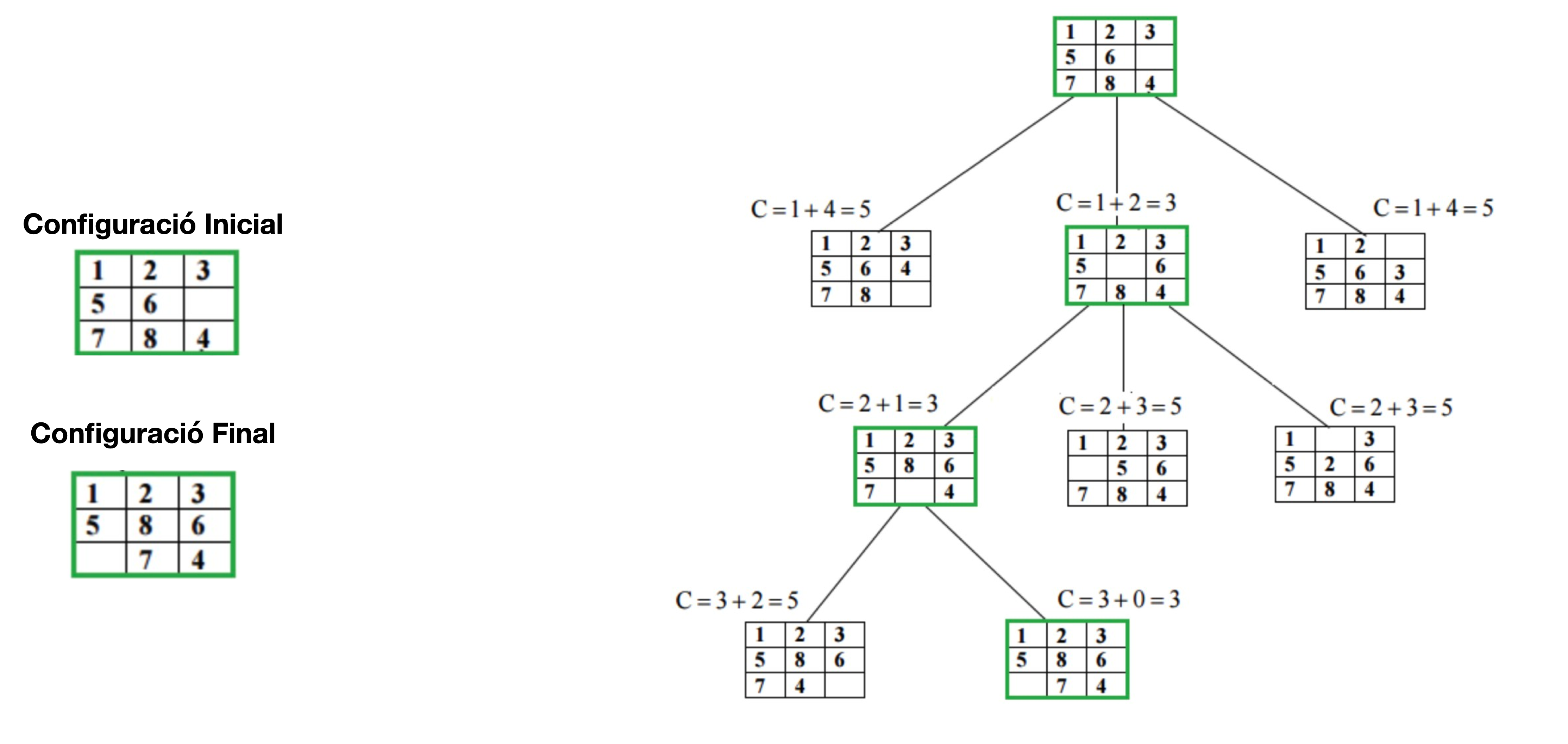
Implementeu l’algorítme de ramificació i poda.