algo2

Sessió en línia del dia 30/11/2020: Programació Dinàmica 2

Exemple: Longest Increasing Subsequence (LIS)

El problema de la seqüència creixent màxima, consisteix amb trobar una subseqüència d’una seqüència donada, tal que els elements de la subseqüència estiguin ordenats, de menor a major, i la subseqüència sigui el més gran possible. Per exemple:

Aquesta subseqüència té longitud 6, i la seqüència d’entrada donada no té cap subseqüència creixent de tamany 7. La subseqüència anterior no és l’única de longitud 6, sinó que podem tindre diverses com per exemple:

La solució d’aquest problema amb programació dinàmica ve donat per la següent funció recurrent:

L(i) = 1 + max(L_0,L_1,...,L_i-1)

amb el cas base:

L(0) = 0

L’algoritme amb programació dinàmica per trobar aquesta solució pot ser el següent:

def lis(A):
    L = [1] * len(A)
    for i in range(1, len(L)):
        subproblems = [L[k] for k in range(i) if A[k]<A[i]]
        L[i] = 1 + max(subproblems,default=0)
    return max(L,default=0)

Mireu el següent vídeo del minut 0.00 fins 9:20:

Exemple: Distància d’edició (levenshtein)

Donades dues paraules per exemple: SNOWY and SUNNY quina és el distancia d’edició?

Cost total = 3

Un altre exemple:

Cost total = 5

Podem definir la seqüència recurrent tenint en compte els següents punts:

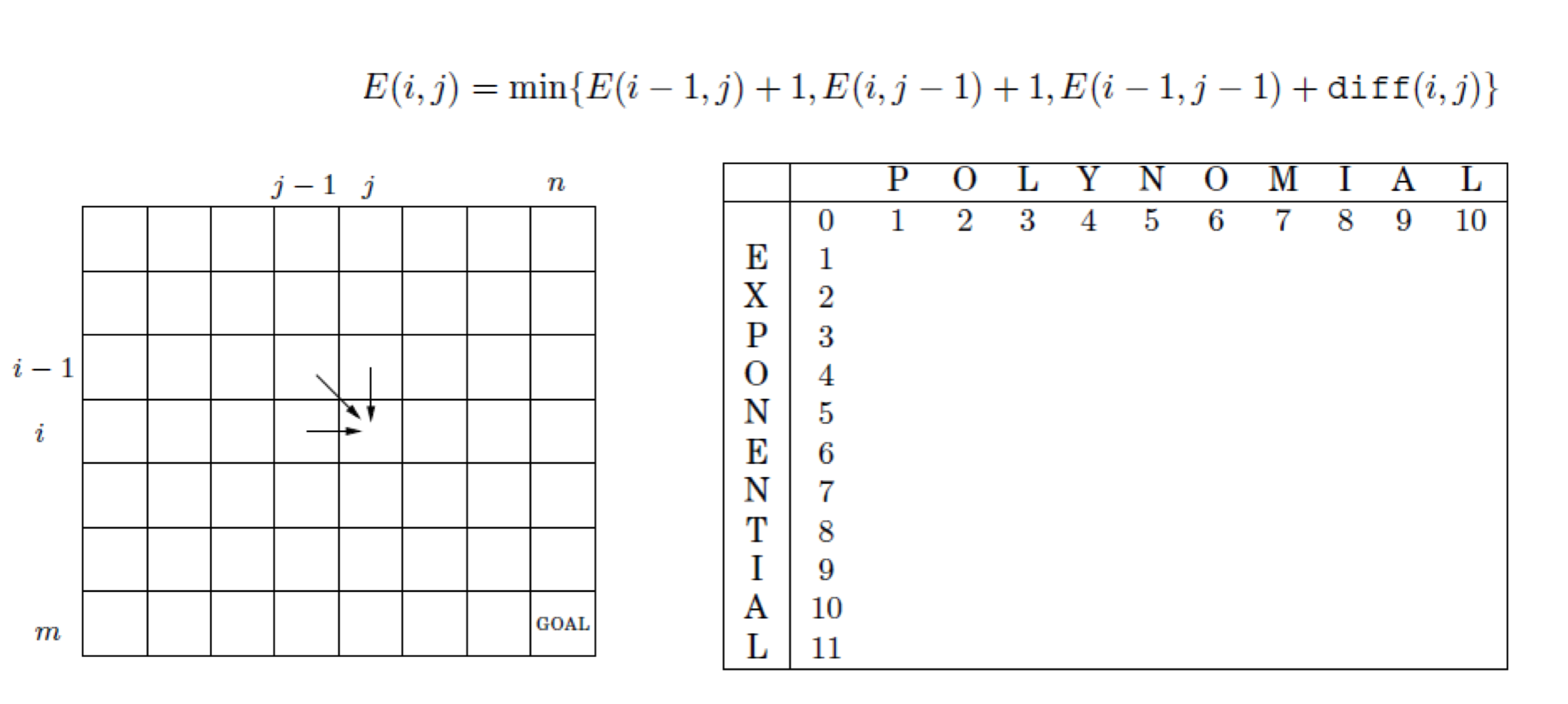
drawing

El cost d’edició de la paraula (POL) per (EXP) vindrà definit per: E(POL,EXP) = min{E(PO,EXP) + 1, E(POL, EX) + 1, E(PO,EX) + dif(L,X)} Si executem aquesta funció recursiva d’esquerra a dreta i de dalt a sota, podem emplenar aquesta taula i obtindrem el següent resultat:

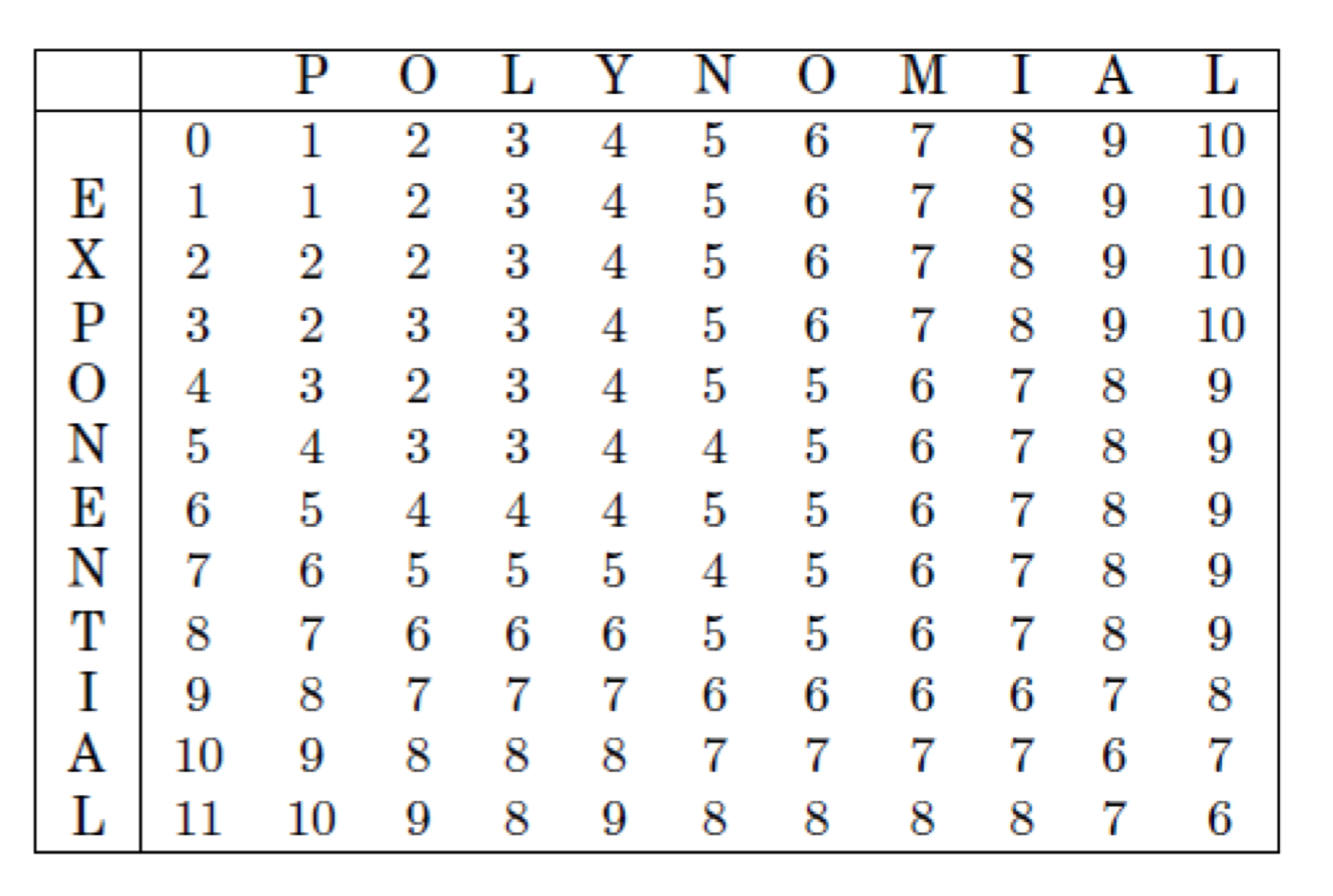
drawing

La solució naïf d’aquest problema podria ser la següent:

def editDistance(str1, str2, m, n):
 
    # Si el primer string té longitud 0 , l'única opció
    # és afegir els caràcters del segon string
    if m == 0:
        return n
 
    # Si el segon string té longitud 0, l'única opció
    # és eliminar els caràcters del primer string
    if n == 0:
        return m
 
    # Si l'últim caràcter dels dos string és el mateix
    if str1[m-1] == str2[n-1]:
        return editDistance(str1, str2, m-1, n-1)
 
    # Si l'últim caràcter dels dos string no és el mateix
    # cridem la funció recusiva de les diferencs accions i agafem la de menor cost+1
    return 1 + min(editDistance(str1, str2, m, n-1),    # afegir
                   editDistance(str1, str2, m-1, n),    # eliminar
                   editDistance(str1, str2, m-1, n-1)   # reemplaçar
                   )
 
 
str1 = "sunny"
str2 = "snowy"
print editDistance(str1, str2, len(str1), len(str2))

La solució d’aquest problema amb programació dinàmica podria ser la següent:

def editDistDP(str1, str2, m, n):
    # Creeam una taula per guardar els resultats
    dp = [[0]*(n + 1) for _ in range(m + 1)]
 
    for i in range(m + 1):
        for j in range(n + 1):
 
            # Si el primer string té longitud 0 , l'única opció
            # és afegir els caràcters del segon string
            if i == 0:
                dp[i][j] = j    
 
            # Si el segon string té longitud 0, l'única opció
            # és eliminar els caràcters del primer string
            elif j == 0:
                dp[i][j] = i    
 
            # Si l'últim caràcter dels dos string és el mateix
            elif str1[i-1] == str2[j-1]:
                dp[i][j] = dp[i-1][j-1]
 
            # Si l'últim caràcter dels dos string no és el mateix
            else:
                dp[i][j] = 1 + min(dp[i][j-1],        # Afegir
                                   dp[i-1][j],        # Eliminar
                                   dp[i-1][j-1])      # reemplaçar
 
    return dp[m][n]
 
 
str1 = "sunny"
str2 = "snowy"
print(editDistDP(str1, str2, len(str1), len(str2)))

Exercici:

Associar la paraula ALGORISMICA amb la paraula AVANÇADA fent ús d’aquesta inicialització i funció de programació dinàmica

Exemple: Viatjant de comerç

EL problema del viatjant de començ consisteix amb trobar un recorregut de longitud mínima per a un viatger que hagi de visitar diverses ciutats i després tornar al punt d’inici, on la distància existent entre cada parella de ciutats és coneguda.

És a dir, donat un graf dirigit amb arestes amb cost positiu, es vol trobar un circuit de longitud mínima que comenci i acabi en el mateix node passant exactament un cop per a cada un dels nodes restants.

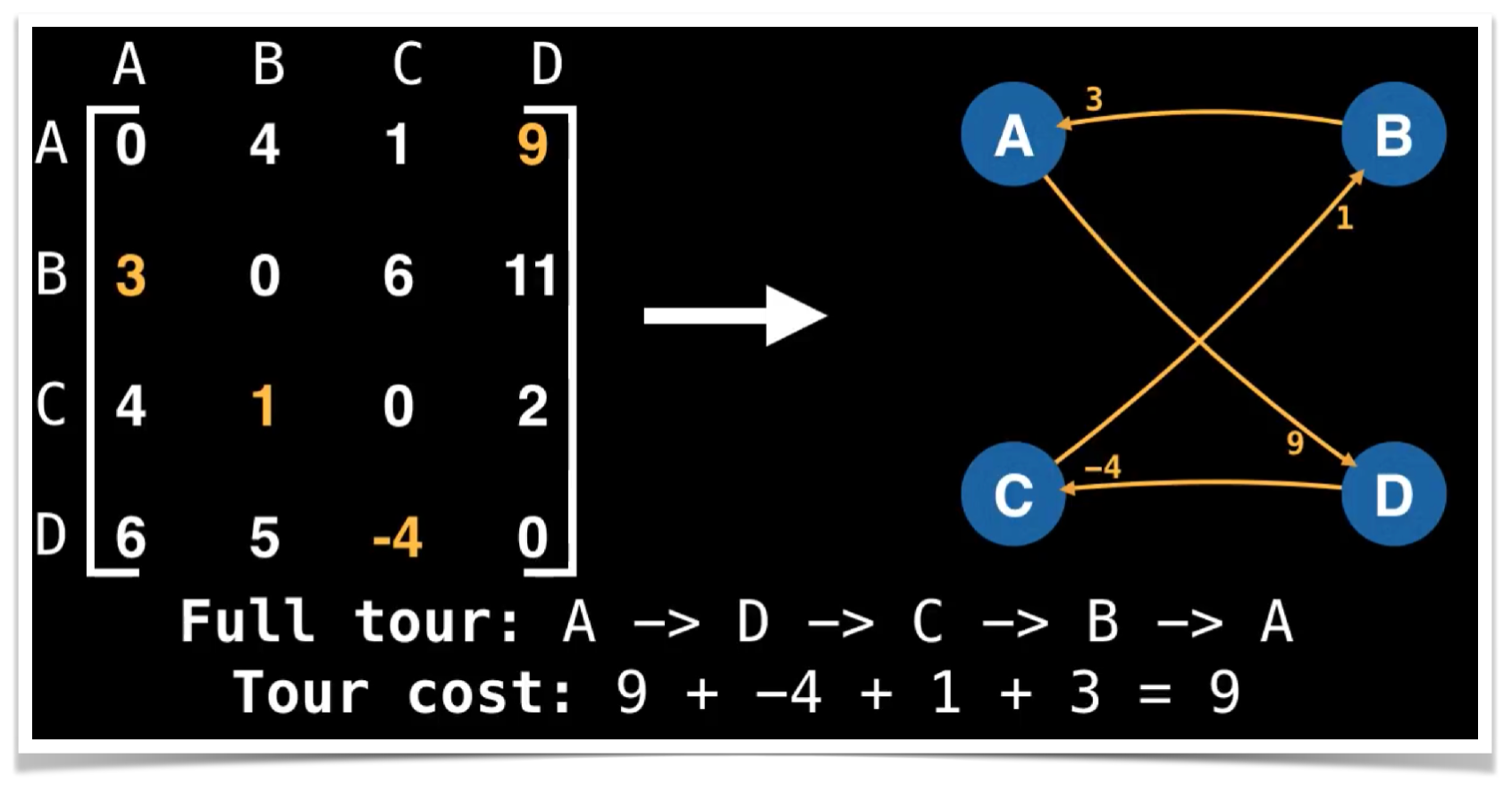
drawing

Aquest problema consisteix amb trobar el circuit Hamiltonià.

Trobar la solució mitjançant una cerca exhaustiva implica mirar totes les possibles permutacions dels nodes ordenats, el que implica una complexitat de complexitat O(n!).

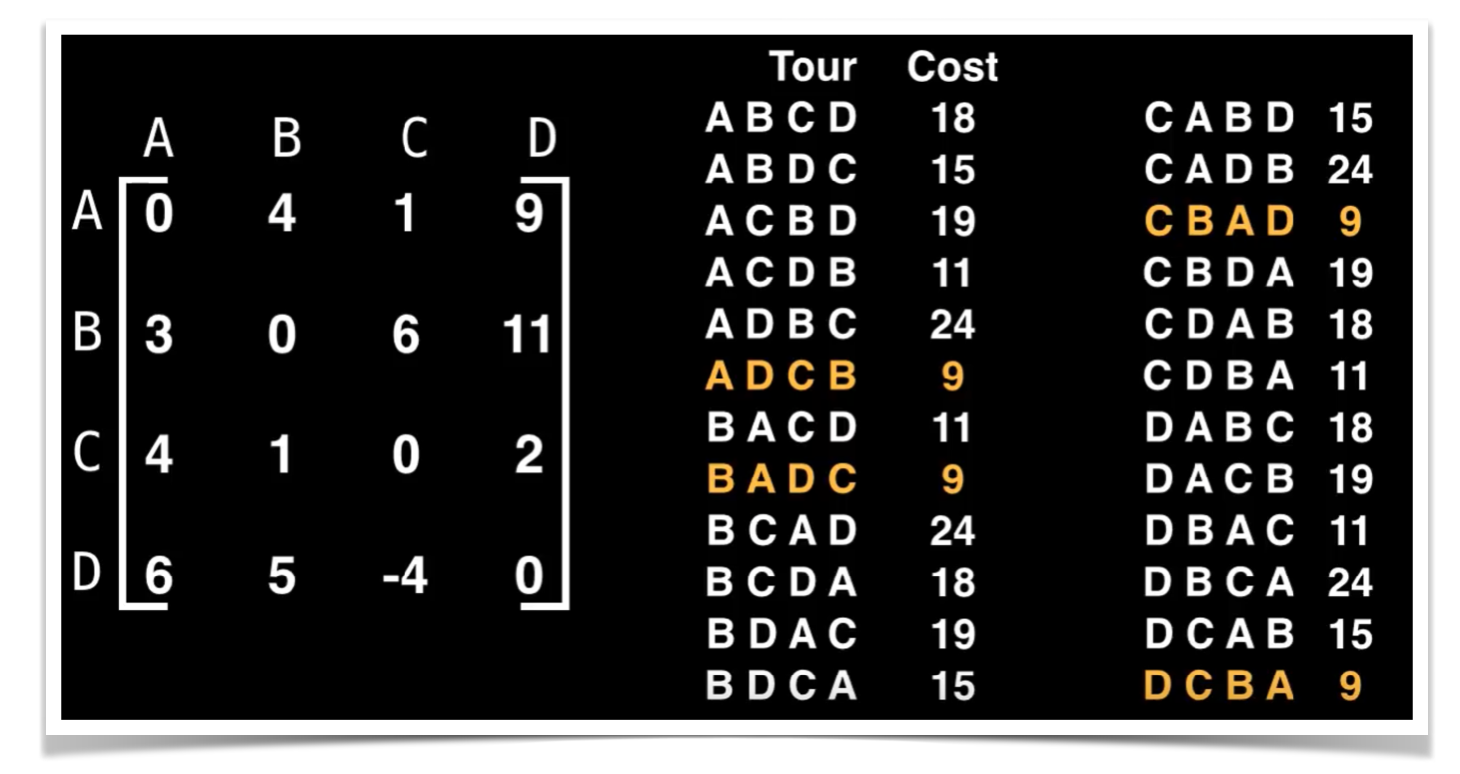
drawing

Tenim una solució mitjançant programació dinàmica que millora significament la complexitat en el temps, passem d’una complexitat O(n!) a O(n^2 2^n)

La idea principal consisteix en calcular la solució òptima per a tots els subcamins de longitud N utilitzant informació que ja coneixem de les solucions parcials òptimes amb longitud N-1

Abans de veure el vídeo intenteu pensar com podríeu solucionar el problema del viatjant de comerç mitjançat Programació Dinàmica.

PISTA: Si D(v_i, S) és la longitud del camí mínim sortint del vèrtex v_i i passant per cadascun dels vèrtexs del conjunt S i tornat al vèrtex v_i. La funció de recurrència es pot definir com: