algo2

Sessió en línia del dia 5/10/2020: Grafs I

Aquesta sessió té una durada aproximada de 60 minuts i està formada per alguns vídeos sobre els aspectes teòrics del tema i diversos exercicis. Es recomana seguir aquests continguts en el mateix ordre que apareixen en aquesta pàgina.

---

Vídeo: Representació

Video de 14’ amb una introducció als grafs i a la representació.

---

---

Exercici 0: RECAP Recorregut Grafs

Donat el següent arbre:

# Using a Python dictionary to act as an adjacency list
graph = {
    'A' : ['B','C'],
    'B' : ['D', 'E'],
    'C' : ['F'],
    'D' : [],
    'E' : ['G'],
    'F' : ['H'],
    'G' : [],
    'H' : []
}

visited = set() # Set to keep track of visited nodes.

def explore(visited, graph, node):
    if node not in visited:
        print (node)
        visited.add(node)
        for neighbour in graph[node]:
            explore(visited, graph, neighbour)

# Driver Code
explore(visited, graph, 'A')

Quina és la sortida del codi anterior? Què fa?

Vídeo: DFS

Vídeo de 10’ sobre l’algoritme DFS

---

Exercici 1: DFS

Quina és la complexitat del DFS implementat mitjançant una llista d’adjacència? Podeu veure el codi a sota.

# Using a Python dictionary to act as an adjacency list
graph = {
    'A' : ['B','C'],
    'B' : ['D', 'E'],
    'C' : ['F'],
    'D' : [],
    'E' : ['F'],
    'F' : []
}

visited = set() # Set to keep track of visited nodes.

def dfs(visited, graph, node):
    if node not in visited:
        print (node)
        visited.add(node)
        for neighbour in graph[node]:
            dfs(visited, graph, neighbour)

# Driver Code
dfs(visited, graph, 'A')

---

Exercici 2: DFS

• Modifiqueu el codi anterior utilitzant la matriu d’adjacència.
• Quina és la complexitat del DFS utilitzant la matriu d’adjacència?

---

Video: BFS

Vídeo de 8’ sobre l’algoritme BFS

---

Exercici 3: BFS

Considerem un Arbre format per N nodes i N-1 arestes on cada node rep un nombre del 1 a N com a identificador únic. Sigui l’1 el node arrel de l’arbre situat nivell 1, fes un programa que, donat un nivell $x$, retorni el nombre de nodes que es trobin en aquest nivell.

Format de entrada:

• La primera línia consisteix en un únic enter N que indica el nombre de nodes de l’arbre. Cadascuna de les següents n-1 línies consta de 2 enters a i b que denoten una aresta no dirigida entre el node a i el node b. La següent línia consisteix en un únic enter x.

Format de sortida:

• Heu d’imprimir un nombre enter únic que indiqui el nombre de nodes del nivell x.

---

Exercici 4: Components connexes

Diem que un graf no dirigit és connex si és possible formar un camí des de qualsevol vèrtex a qualsevol altre en el graf. Una component connexa d’un graf no dirigit és un subgraf connex maximal. Cada vèrtex i cada aresta pertany a una única component connexa.

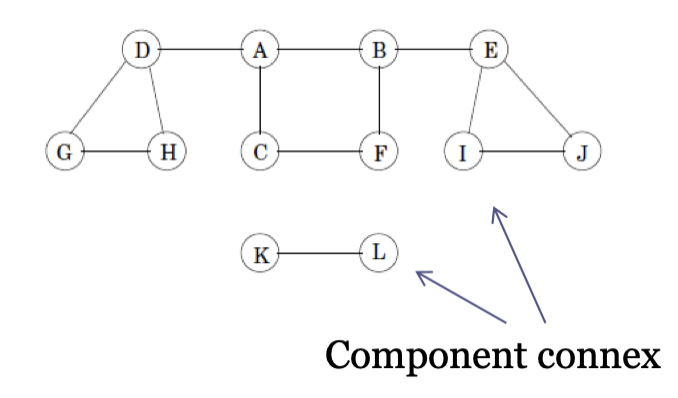
Exemple: Graf no dirigit no connex, 12 vèrtexs,13 arestes i dues components connexes

Implementeu una funció que identifiqui les diferents components connexes d’un graf.

• Utilitzeu el mètode DFS per tal de trobar la solució.

---

Exercici 5: Graf dirigit fortament connex

Un graf dirigit s’anomena fortament connex quan, donats dos vèrtexs qualssevol u, v, conté un camí dirigit de u a v i un camí dirigit de v a u. Una component connexa forta és un subgraf maximal fortament connex.

Implementeu una funció que identifiqui si un graf dirigit és fortament connex.

---

Exercici 6: Graf dirigit feblement connex

Un graf dirigit s’anomena feblement connex quan és connex com a graf no dirigit. És a dir, quan en substituir totes les seves arestes (dirigides) per arestes no dirigides obtenim un graf no dirigit connex.

Implementeu una funció que identifiqui si un graf dirigit és feblement connex.